UNIDAD: 6
EL PLANO CARTESIANO
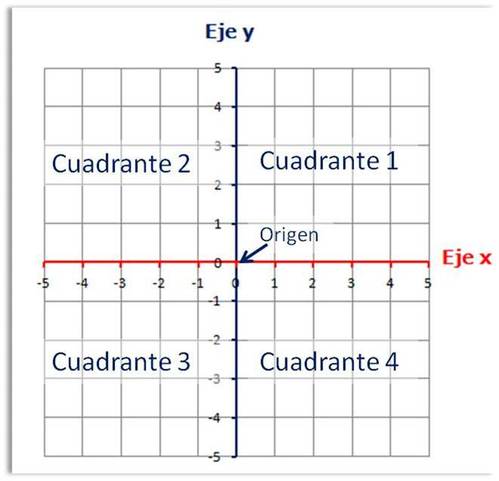
El plano cartesiano está formado por dos rectas numéricas, una horizontal y otra vertical que se cortan en un punto. La recta horizontal es llamada eje de las abscisas o de las equis (x), y la vertical, eje de las ordenadas o de las yes, (y); el punto donde se cortan recibe el nombre de origen.

El plano cartesiano es un diagrama en el que podemos ubicar puntos, basándonos en sus coordenadas respectivas en cada eje, tal y como hace un GPS en el globo terráqueo. De allí, también es posible representar gráficamente el movimiento (el desplazamiento de un punto a otro en el sistema de coordenadas).
Además, permite trazar figuras geométricas bidimensionales a partir de rectas y curvas. Estas figuras se corresponden con determinadas operaciones aritméticas, como ecuaciones, operaciones simples, etc.
Cuadrantes del plano cartesiano
Cuadrante I, en la región superior derecha, en donde pueden representarse valores positivos en cada eje de coordenadas. Por ejemplo: (1,1).
Cuadrante II, en la región superior izquierda, en donde pueden representarse valores positivos en el eje y pero negativos en el x. Por ejemplo: (-1, 1).
Cuadrante III, en la región inferior izquierda, en donde pueden representarse valores negativos en ambos ejes. Por ejemplo: (-1,-1).
Cuadrante IV, en la región inferior derecha, en donde pueden representarse valores negativos en el eje y pero positivos en el x. Por ejemplo: (1, -1).
ACTIVIDAD : LOCALIZAR EN EL PLANO CARTESIANO; CUADRANTES, EJE X, EJE Y PARTE POSITIVA Y NEGATIVA (LOCALIZANDO NÚMEROS DEL 1 AL 10.
VÍDEO COMPLEMENTARIO ; OBSERVAR
SISTEMA DE COORDENADAS
Observar el vídeo
Observar el vídeo
ACTIVIDAD: LOCALIZAR LOS SIGUIENTES PARES ORDENADOS EN EL PLANO CARTESIANO.

QUE ES UNA RELACIÓN MATEMÁTICA?
Observar el vídeo Y tomar apuntes.
Ejemplos de relaciones matemáticas


ACTIVIDAD: REALIZAR UN EJERCICIO DE RELACIÓN MATEMÁTICA, SEGÚN LO QUE ENTENDIÓ.
QUÉ ES UNA FUNCIÓN MATEMÁTICA
EJEMPLOS DE FUNCIONES

ACTIVIDAD: ANALIZA LOS SIGUIENTES EJERCICIOS SI ES FUNCIÓN O RELACIÓN.
UNIDAD 7: FUNCIÓN LINEAL
QUÉ ES FUNCIÓN LINEAL?
Las funciones lineales se representan con una línea recta en el plano cartesiano. Es importante tener en cuenta que lo que hacen las funciones, en definitiva, es expresar una relación entre variables, pudiéndose desarrollar modelos matemáticos que representen este vínculo.
El conjunto de partida o conjunto inicial se lo denomina dominio, mientras que al conjunto de llegada o conjunto final se lo llama codominio. Las variables independientes forman parte del dominio; las variables dependientes, del codominio. Cuando a los cambios iguales de una variable independiente le corresponden variaciones iguales de la variable dependiente, se habla de función lineal.
OBSERVAR EL VÍDEO
CÓMO GRAFICAR FUNCIONES LINEALES?
REPASO: OBSERVAR EL VÍDEO.
ACTIVIDAD: DESARROLLAR LAS SIGUIENTES EJERCICIOS DE FUNCIONES LINEALES Y GRAFICARLAS.
A. y = 2x − 1
B. y = 2x
C. y = 2x + 3
RECTAS PARALELAS, PERPENDICULARES Y SECANTES
QUÉ ES UNA RECTA?
En geometría euclidiana, la recta o la línea recta es una línea que se extiende en una misma dirección; por lo tanto, tiene una sola dimensión y contiene un número infinito de puntos. Dicha recta también se puede describir como una sucesión continua de puntos extendidos en una sola dirección.
Las rectas no tienen comienzo ni final: son líneas compuestas de puntos que se suceden de manera indefinida. Están consideradas como uno de los entes fundamentales de la geometría, al igual que los ya mencionados puntos y los planos.

QUÉ SON RECTAS PARALELAS, PERPENDICULARES Y SECANTES?
OBSERVAR EL VÍDEO Y TOMAR APUNTES
ACTIVIDAD : REALIZAR EJEMPLOS DE LINEAS PARALELAS, PERPENDICULARES Y SECANTES.